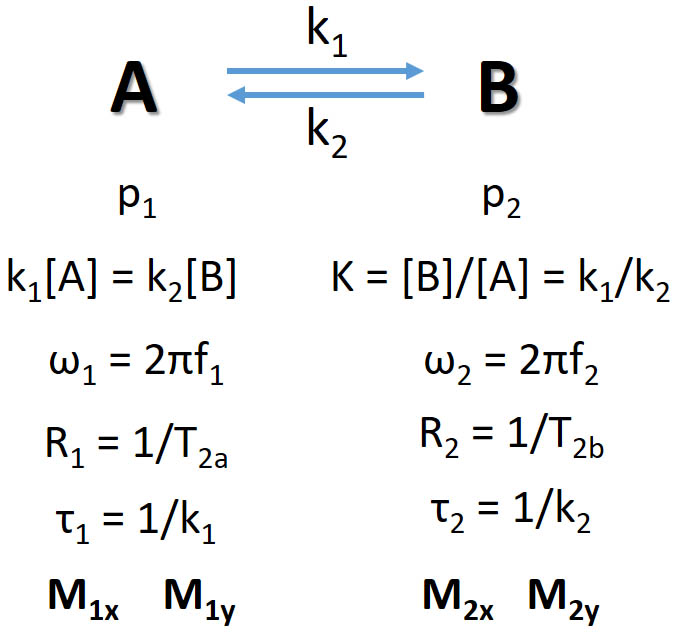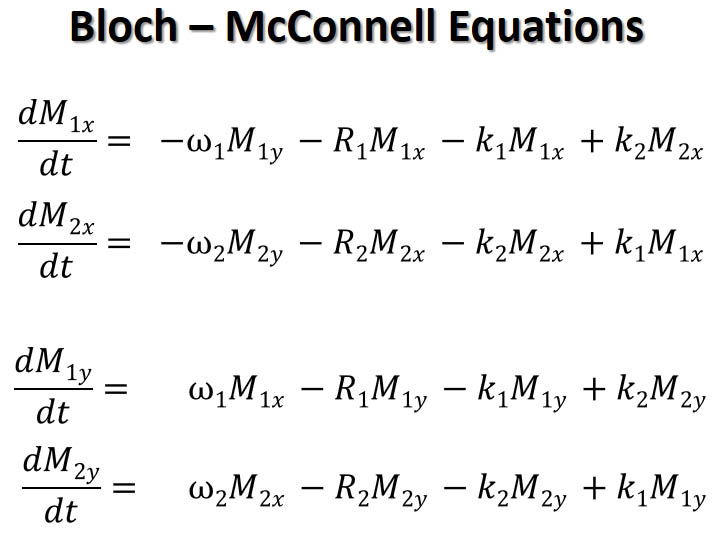NMR Theory, UCSB Chem and Biochem NMR Facility

NMR Theory and Techniques

Note: During training and assisting students and researchers, I often find it helpful to go over some NMR theory which is usually picked up in bits and pieces sporadically over the years for most users. Evidently, this work has evolved into a much bigger project in a short time. I hope these materials will spur more interest in NMR and help all users, especially new ones, to broaden their skills and understanding of the NMR techniques. Some data shown here are synthesized, perfect data for illustration purposes. The data are generated with in-house written Tcl/Tk scripts, converted to nmrPipe binary data, and then processed with Mnova. Many common NMR terminologies are highlighted in bold. Since other aspects of the NMR techniques are covered in various lab classes, focus is given here to better understanding the mathematical and physical basis of various NMR observations and techniques. Some are very relevant to routine practice, especially in the design of NMR experiments and data interpretation. -- Hongjun Zhou, @UCSB, 01/2019

"I insist upon the view that 'all is waves'."
-- Erwin Schrödinger in Letter to John Lighton Synge (1959)

Transient NOESY: A Better Method of Measuring NOEs

Pulsed Field Gradients (PFG): Now You See It, Now You Don't

Chemical Exchange

The term chemical exchange originally refers to exchange processes between different molecules. However, it is now often used to broadly describe any general exchange processes relevant to NMR. Here we use "chemical exchange", sometime simply exchange, for all mechanisms that cause a nuclear spin to change among a set of discrete chemical environments, with or without an associated change in its chemical shift or frequency. The "discrete states" notion is to differentiate this exchange from more rapid, more random thermal molecular motions on the pico- to nano- second time scale.

Exchange is widely encountered in NMR analysis and is one of the most interesting, widely explored phenomena that often reveal very interesting biological functions associated with the dynamic properties of the molecules. Examples of these exchanges include structural switching between conformers, on/off events of ligand binding, spontaneous or ligand-induced motions that are relevant to the molecular function, protonation and deprotonation, hydrogen-deuterium exchange, among many others. Solution-state NMR is especially useful in this type work because many interesting exchange events fall within a time regime (microsecond to hours) that NMR experiments can be conducted, can be done in real time and in situ, and can be analyzed along with a wealth of other NMR data that can be collected off the same sample or system.

Measurements of the exchange rates, and isolation and characterization of individual states through NMR signal lineshape analysis and more recently through exchange spectroscopy (EXSY) have widespread use in kinetics and molecular function studies. There has been a large number of publications on the subject since the late 1940s. Two books that have a good amount of coverage on the subject are "Dynamic NMR Spectroscopy (1982)" by J. Sandstrom and "Principles of Nuclear Magnetic Resonance in One and Two Dimensions (1987)" by R. Ernst, G. Bodenhausen and A. Wokaun. More recent developments on the subject can be found in many review articles, such as "Chemical Exchange in NMR" (Progress in Nuclear Magnetic Resonance Spectroscopy, Vol. 43, pages 63-103 by A. Bain). The mathematical and physical descriptions of the exchange impacts on NMR signals have been mostly worked out for two-site exchange. For more than two sites, the details often can only be solved numerically due to the complexities of the analytical solutions and the difficulty of separating the real and imaginary parts analytically. Approximations or simple assumptions are often made to reduce the general analytical solutions to simple formulas to help gain insight into the exchange phenomena.

It is important to note there are two distinct "exchange" events: one is the underlining chemical one which is not affected by NMR pulsing and manipulation, and the other is the process of the spin transfer between the various states. The NMR exchange process is governed by the kinetics and the initial spin states depending on how the NMR experiment is done. Here we will only consider the cases where the chemical reaction or the exchange is at equilibrium, but the NMR equilibration processes may not be because the two processes are governed separately on two totally diferent, unrelated time scales. We will also ignore spin-spin coupling and only include the Larmor procession of the spins under the static field. For systems not at equilibrium, more complexities are introduced. See the book above by Ernst et al and a nice treatment of the subject by R. O. Kühne, T. Schaffhauser, A. Wokaun, and R.R. Ernst. Study of transient chemical reactions by NMR. Fast stopped-flow fourier transform experiments. J. Magn. Reson. 35 (1979), 39-67.

Consider a "simple" case of two-site exchange where spin S goes between two sites A and B. The relevant parameters are summarized in the figures above. They are the forward and backward rates k₁ (A→B) and k₂ (B→A), the fractional populations of the spin p₁ and p₂ (with p₁ + p₂ = 1), the resonance angular frequencies ω₁ and ω₂, the transverse relaxation rates R₁ and R₂ which are inverse of the time constants, and the residence lifetimes of the two sites τ₁ and τ₂. We use M_1x, M_1y, M_2x, M_2y to represent the exchangeable X and Y magnetizations of the spin at the two sites. Note k₁ and k₂ are related to the equilibrium constant k and concentrations. When A and B are at equilibrium, we have k₁[A] = k₂[B].

Under chemical exchange and free signal procession around the static field B_z, the NMR signal evolution is described by the macroscopic Bloch-McConnell equations above which couple free procession of the nuclear spins with chemical exchange. An analytical solution to the eigenstates of the XY and Z components of the magnetizations can be found in J.S. Leigh Jr., Relaxation times in systems with chemical exchange: some exact solutions, J. Magn. Reson. 4 (1971) 308-311, and J. Sandstrom "Principles of Nuclear Magnetic Resonance in One and Two Dimensions (1987)" among other publications. The real and imaginary parts from the general solutions, however, are entangled due to the exchange and are not generally separable analytically if the system involves more than two sites. Approximations are often necessary for fitting experimental results to extract model parameters.

The figures below illustrate some commonly encountered situations and observations under two-site exchange. These spectra are generated from direct, numerical solutions to the Bloch-McConnell equations above.

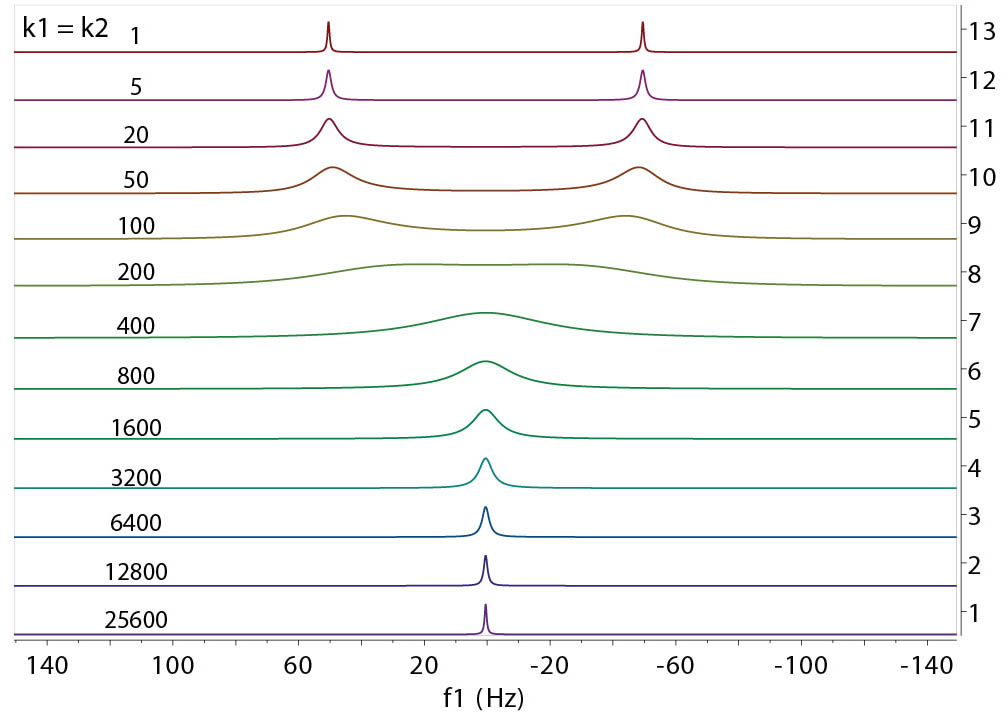
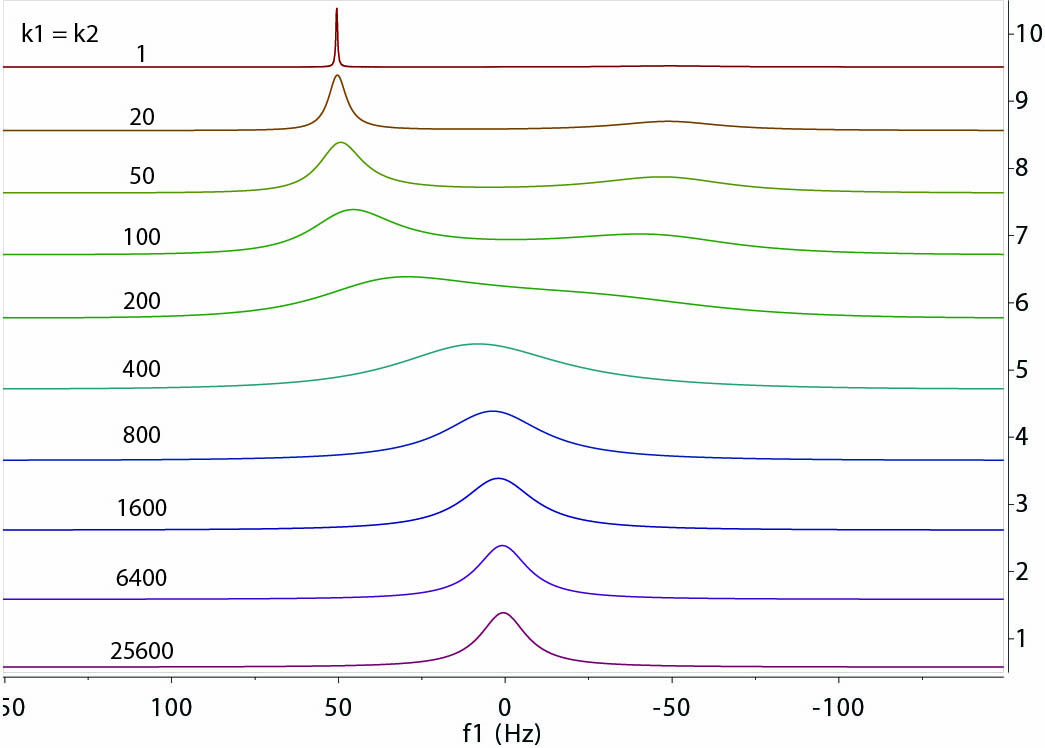
The example above shows the impact of the exchange of various rates on the resonances from the spins at site A and site B under equilibrium condition. The following parameters were used in the computation: f₁ = -50 Hz, f₂ = +50 Hz, transverse relaxation times T_2A = T_2B = 1.0 sec, and population ratio p_A:p_B = 1:1. The rates of exchange (k₁=k₂, per sec) are given in the graph. They range from very slow relative to |f₂ - f₁| ~ 100 Hz to very fast.

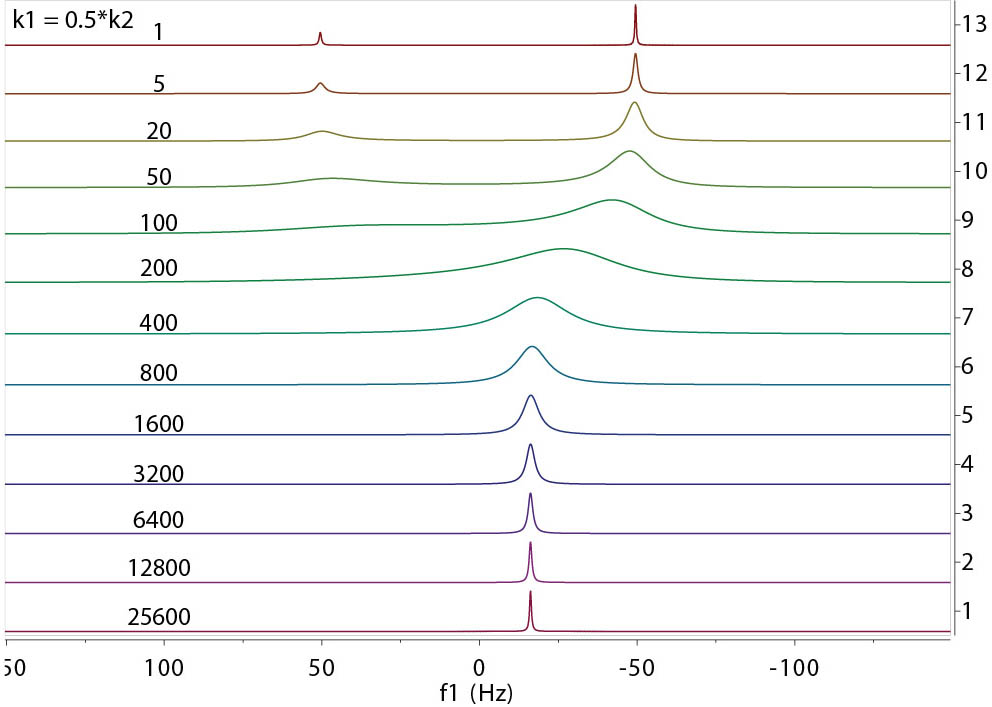
Above is another example with the population ratio between A and B at 2:1 and the k₁ rates indicated. From the examples, a few general observations can be made.

The peak lineshape is highly dependent on the relative exchange rates (or time-scale) of the exchange involved. The exchange rates can be divided into slow, intermediate, and fast realtive to the frequency differences (in Hz) of the exchangeable resonances.
Slow exchange: The peaks are separated and are as sharp as those without exchange. Their intensities (integrals) are proportional to the population of each site.
Intermediate exchange: This is where the peaks start to broaden with an envelope roughly in proportion with the range of the frequency differences between the sites. The peaks may disappear entirely in extreme cases.
Fast exchange: Peaks start to sharpen and merge towards to a single, population weighted, average position between the sites. The linewidth of the peak shows an average width of the separate peaks of individual sites.

The exchange rate characterization can be equally made with time scale. A 1000 Hz exchange rate is roughly on the time scale of 1/1000 sec or 1 msec. It is interesting to note that the same underlining exchange broadens peaks from different nuclei by a different amount because the separation frequency, measured in Hz, between the exchangable sites depends on γ as well as field strength. This means a ¹H signal may still be present but ¹³C signal from the same group may be absent due to severe broadening. This differential broadening should lead to a range estimate for the rate of exchange. Varying temperature, solvent, or collecting data under a different field may help tilt the rate of exchange towards more observable signals.

Below are some other cases with diverse resonance appearance.

The figure above is from two equally populated sites, but one site has a very short relaxation time. T_2A=0.01 sec, T_2B=1.0 sec. The peak at -50 Hz is very broad by itself with a linewidth of 1/(πT₂) ~ 32 Hz and is barely visible in the top trace at this scale. This situation may be created when the molecule interacts with a paramagnetic ion. When one of the sites has a large linewidth (short relaxation time) and not well observed by itself, the observed exchange-broadened peak (left peak) may show broadening under moderate slow exchange that mimics the situation of "intermediate" exchange of two sharp signals. Care must be taken to draw conclusion. Variation of temperature or concentrations of the additives may help resolve the ambiguity.

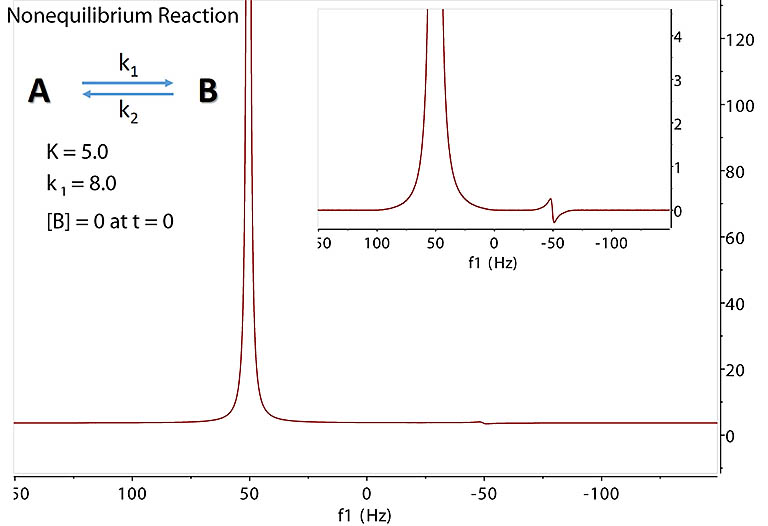
Nonequilibrium Exchange

We move on to more complex nonequilibrium, transient reactions where the populations of A and B spins change as the fast reaction takes place with forward and backward rates k₁ and k₂, respectively. The same Block-McConnell equations above apply. With initial concentration of B at zero, with the equilibrium constant K = 5.0, depending on the other parameters, we may see a small product signal of dispersive shape as shown below by following the reaction during the initial seconds. Note the small dispersive signal at -50 Hz for B spins. This expected observation has been well demonstrated by R. O. Kühne et al (1979) with fast stopped-flow experiments. The dispersive contribution from B to A is not obvious due to the small amount of B and the dominant absorptive peak of A in the unimolecular reaction.

When the reaction is slow with respect to the data collection time, the NMR observation reduces to the equilibrium state situation where each data point is collected with close to fixed concentrations of A and B, and the dispersive peak shape won't be observable. In these cases, the intensities of the initial and final product signals can be tracked over time and fit with a kinetic model to extract K, k₁ and k₂.

References on Chemical Exchange:

H.M. McConnell. Reaction rates by nuclear magnetic resonance. J. Chem. Phys., 28 (1958), pp. 430-431.
J.S. Leigh Jr., Relaxation times in systems with chemical exchange: some exact solutions.J. Magn. Reson., 4 (1971), pp. 308-311.
Hansen, D & Led, Jens. Implications of using approximate Bloch-McConnell equations in NMR analyses of chemically exchanging systems: Application to the electron self-exchange of plastocyanin. J. Magn. Reson. 163 (2003), pp. 215-227.
R. O. Kühne, T. Schaffhauser, A. Wokaun, and R. R. Ernst. Study of transient chemical reactions by NMR. Fast stopped-flow fourier transform experiments. J. Magn. Reson. 35 (1979), 39-67.
I. Solomon, Relaxation Processes in a System of Two Spins. Phys. Rev. 99 (1955), 559.

Updated, Jan-Feb 2019, Hongjun Zhou