NMR Theory, UCSB Chem and Biochem NMR Facility

NMR Theory and Techniques

Note: During training and assisting students and researchers, I often find it helpful to go over some NMR theory which is usually picked up in bits and pieces sporadically over the years for most users. Evidently, this work has evolved into a much bigger project in a short time. I hope these materials will spur more interest in NMR and help all users, especially new ones, to broaden their skills and understanding of the NMR techniques. Some data shown here are synthesized, perfect data for illustration purposes. The data are generated with in-house written Tcl/Tk scripts, converted to nmrPipe binary data, and then processed with Mnova. Many common NMR terminologies are highlighted in bold. Since other aspects of the NMR techniques are covered in various lab classes, focus is given here to better understanding the mathematical and physical basis of various NMR observations and techniques. Some are very relevant to routine practice, especially in the design of NMR experiments and data interpretation. -- Hongjun Zhou, @UCSB, 01/2019

"I insist upon the view that 'all is waves'."
-- Erwin Schrödinger in Letter to John Lighton Synge (1959)

Transient NOESY: A Better Method of Measuring NOEs

Pulsed Field Gradients (PFG): Now You See It, Now You Don't

DOSY: Diffusion Ordered Spectroscopy

The goal of DOSY is to differentiate NMR signals from a mixture of molecules by the differences in their molecular translational diffusion. DOSY has found wide applications in routine NMR analysis of chemical mixtures for chemical identification and quantification. It can also be used as an editing technique similar to isotope editing to separate signals with 2D and 3D experiments. The same technique is also used for measuring molecular diffusion coefficient of a pure sample or estimate molecular size by the measured diffusion coefficient. Any nucleus can be monitored in DOSY with sensitivity as the limiting factor. Commonly used nuclei include ¹H, ¹⁹F and ³¹P (Wang et al 2017).

The diffusion coefficient is affected by molecular size and shape with additional factors from temperature, solvent viscosity, etc., according to the Debye-Einstein equation:

where the molecule is approximated as a spherical particle of hydrodynamic radius r_H in a solvent of viscosity η; k_B is the Boltzmann constant, and T is the absolute temperature (^ºK). Intuitively, since the molecular radius scales with the molecular weight M_w as: r ∝ M_w^1/3, we would expect the diffusion coefficient D scales with 1/M_w^1/3, but D is close to a linear relationship with 1/M_w within a range. Generally, this scaling should be D ∝ D₀ + M_w^α with α variable depending on the solvent and type of molecules. This deviation likely has to do with the generally nonspherical shape of small molecules, hydration or solvent coating the molecule, interactions with the solvent, etc. making the molecule effectively bigger. This variation suggests a simple, general scalng may not exist over a broad range of molecules and therefore requires that in order to use diffusion coefficient for molecular size determination a calibration must be done for each class of solvent and molecules. See examples from this article, more here and here.

A large collection of literature is available on DOSY techniques and applications. For a review by one of the DOSY pioneers, see C.S. Johnson Jr. (1999) Diffusion ordered nuclear magnetic resonance spectroscopy: principles and applications. Prog. Nucl. Magn. Reson. Spectrosc. 34, 203. and the original publication on DOSY: K.F. Morris, C.S. Johnson Jr. (1992) Diffusion-Ordered Two-Dimensional Nuclear Magnetic Resonance Spectroscopy. J. Am. Chem. Soc. 114, 3139.

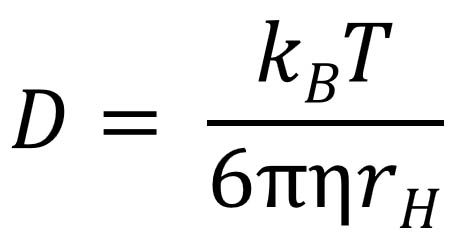
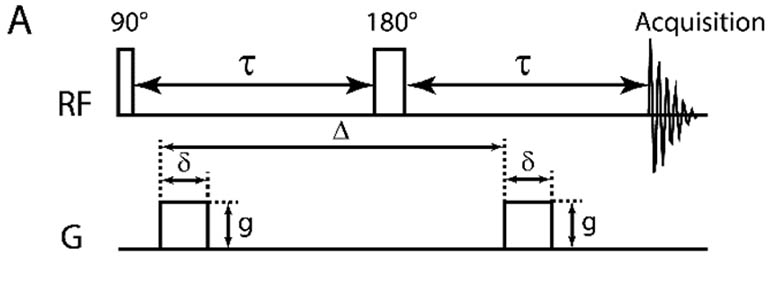
A simple DOSY pulse sequence using a spin echo (SE). The 90-degree pulse flips the spins into the transverse plane followed by position/phase encoding by the gradient pulse. The 180 degree pulse reverses the sign of the phase changes from the first gradient pulse, which are subsequently canceled by the second gradient pulse unless the spins have diffused over the delay period Δ. The loss of the signal intensity as a function of diffusion delay is measured and processed. In this experiment, diffusion occurs while the spins are in the transverse XY plane. As usual, chemical shift evolution, but not homonuclear J-coupling, is refocused at the beginning of the echo by the 180-degree pulse.

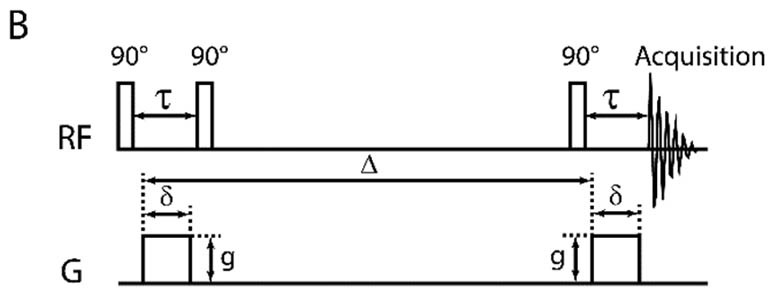DOSY with stimulated spin echo (STE). The first 90-degree pulse flips the spins into XY plane. The first gradient then encodes the spins with position dependent phase changes before the second 90-degree pulse flips the spatially labeled spins to Z for diffusion over Δ delay. The third 90-degree pulse flips the stored spins back into XY plane. The second gradient cancels the phase changes done by the first one and enables an echo, leaving only the signal amplitude drop from diffusion. The last two 90-degree pulses act like a 180-degree pulse to reverse the spin phase changes by the gradient pulses to form the echo.

A DOSY experiment uses a spin echo, either the simple Carr-Purcell spin echo (SE) (also called the Hahn echo) or stimulated echo (STE), which "refocuses" the dephasing effects of the gradients weighted by the amount of diffusion. The advantage of STE is that magnetization is stored along Z during the diffusion period (Δ) to take advantage of longer T₁ than T₂, especially for macromolecules. This substantially reduces the loss of sensitivity when the spins diffuse while they are transverse. This is beneficial in most cases even considering there is a loss of half of the magnetization from the second 90-degree pulse because only the spins along either X or Y axis are flipped to Z. Most DOSY pulse sequences in use have more pulses than the ones shown above to deal with gradient stabilization, fluid convection and artifact removal.

Practically, the diffusion effect is detected in a series of 1D experiments with varying gradient strength rather than the diffusion time so that relaxation is a constant during diffusion, and therefore is factored out. The peak amplitudes in the arrayed spectra are fit with the Stejskal-Tanner formula:

S(G_z) = S(0)*exp(- Dγ²G_z²δ²(Δ - δ/3))

where S(G_z) is the measured peak intensity with gradient G_z, S(0) is the intensity when G_z = 0, D is the diffusion coefficient or diffusion constant, γ is the gyromagnetic ratio, δ is the gradient duration, and Δ is the time of diffusion. We can see that measuring diffusion through low γ nuclei is also limited by the weaker effect on the peak intensity; that is compensated by their typically longer T₁ and T₂ and the ability to prolong the diffusion peroid Δ. The diffusion data can be fit peak by peak in a typical curve fitting routine, or processed in a 2D fashion through a Laplace transform (similar to FT but with real values) along the diffusion dimension. 2D presentation has the advantage of easier identifying peaks with the same diffusion coefficients. However, the intuitive simplicity of curve fitting against the equation above is undeniable when precise diffusion coefficient, not particularly molecular separation of a mixture is desired or when ambiguity arises.

Magnetogyric Ratios of Commonly Detected Nuclei^* (γ, unit: 1000 rad·s^-1·G^-1)

Nucleus	γ
1H	26.7522128 (26752.2128 rad·s^-1G^-1)
2H	4.10662791
7Li	10.3977013
11B	8.5847044
13C	6.728284
15N	-2.712618
19F	25.18148
23Na	7.0808493
29Si	-5.3190
31P	10.8394

*Adapted from IUPAC Recommendations 2001

Other Typical, Instrument and Pulse Sequence Dependent Parameters Used in DOSY

Diffusion duration, Δ (sec): 0.05 for very small molecules to 0.5 sec for large polymers
Gradient duration, δ (sec): 0.002 to 0.005
Gradient conversion factor (DAC to Gauss/cm) used on Varian instruments: ~ 0.002. For example, for gradient value 20000 in DAC unit, the strength is 20000 X 0.002 = 40 (Gauss/cm).

Due to the difficulty in calibrating a perfectly linear gradient and conversion of DAC unit to Gauss/cm unit, and solvent viscosity and convection issues, when accurate or absolute diffusion coefficient is desired, using an internal standard, ideally with a well known diffusion value, is very helpful so that all other diffusion coefficients can be scaled against it. However, for mixture separation, absolute diffusion value isn't important.

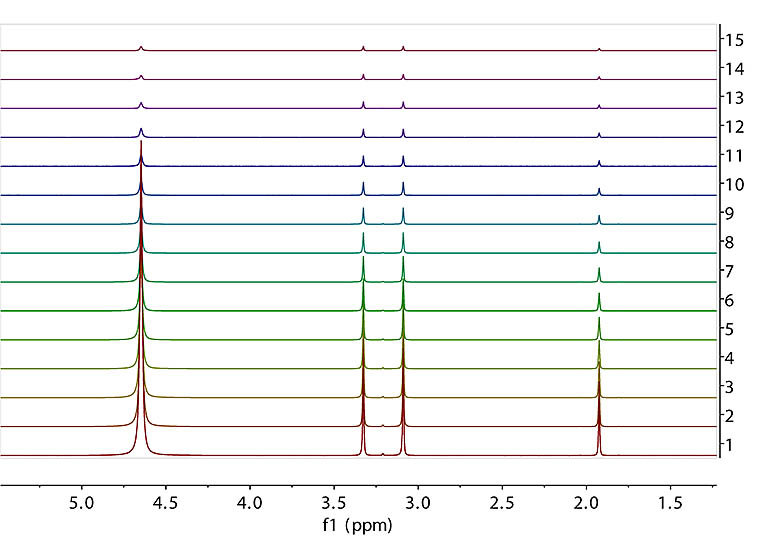DOSY FID array with varying gradient strength and fixed diffusion time. Data were collected on our 600 MHz spectrometer with Varian's DgcsteSL_cc sequence from a sample of 1% H₂O (~4.7 ppm), 0.1% ¹³C labeled methanol (doublet at ~ 3.3 ppm), and 0.1% ¹⁵N labeled acetonitrile (~ 2ppm) in 99% D₂O. From bottom to top, the gradient strength is set to 500, 8039, 11358, 13906, 16055, 17948, 19660, 21234, 22699, 24075, 25377, 26615, 27798, 28933 and 30025 in DAC unit. The maximum gradient (~ 70 Gauss/cm) has a DAC value of 32768. The diffusion time (Δ) is ~ 30 msec.

Recommended signal decay range to measure is from ~ 90% of full intensity with the weakest gradient down to ~ 10% with the maximum gradient.

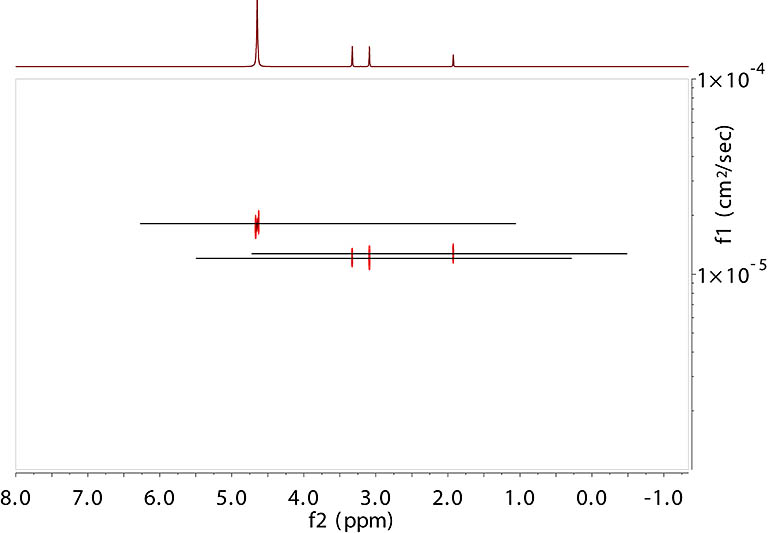Processed DOSY spectrum. The vertical axis is the diffusion coefficient (uncalibrated). Data are processed with Mnova using its Bayesian method.

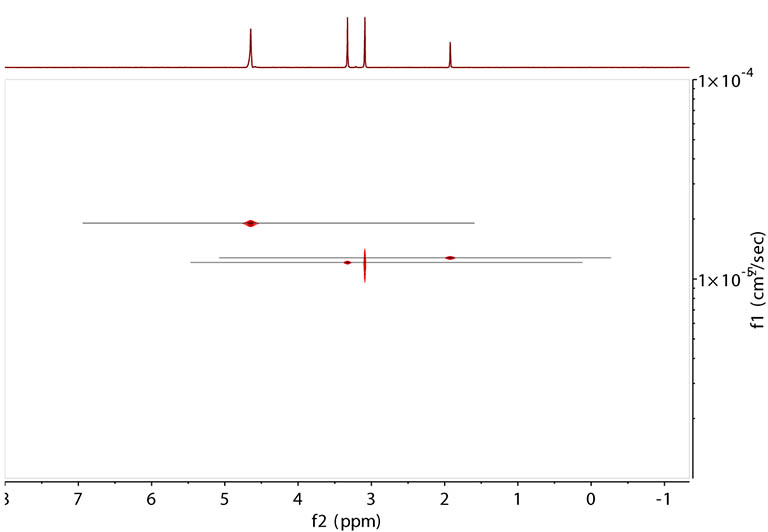Same data processed with the alternative peak fitting method in Mnova.

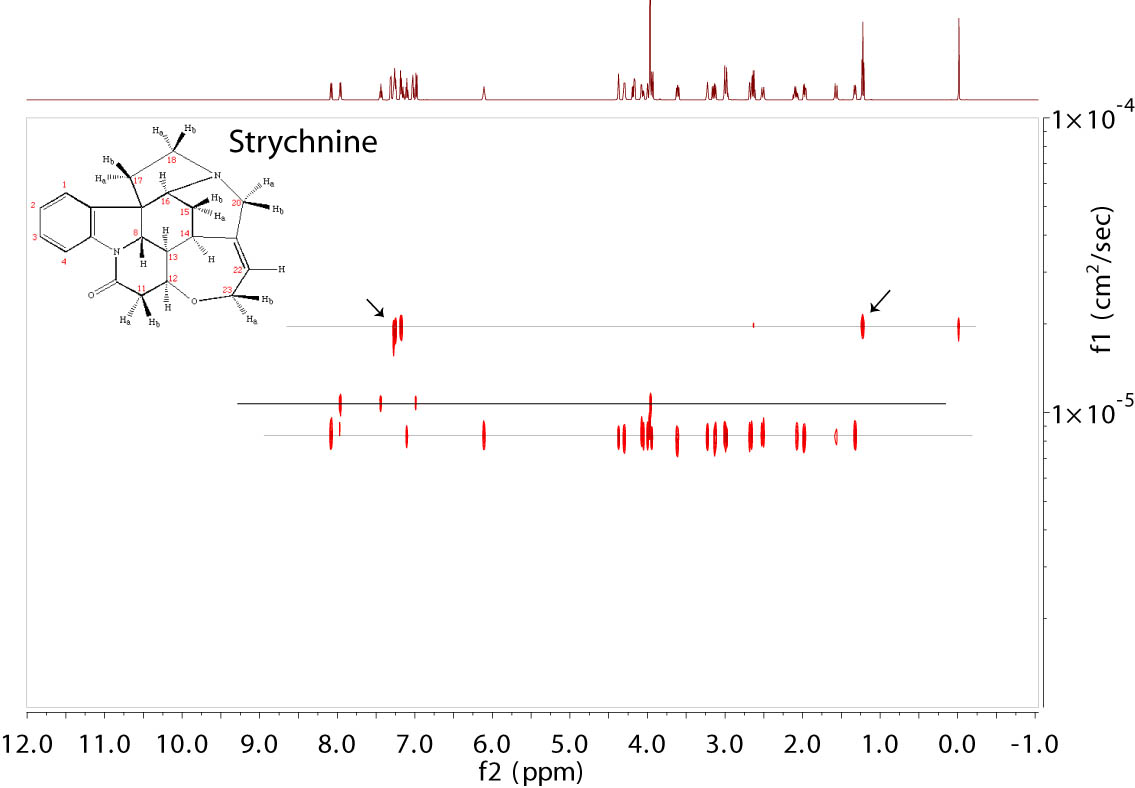DOSY from a Strychnine sample in CDCl₃. The chemical had decomposed and gave several extra peaks from the decomposed product marked by the solid line and arrows along the top line. TMS was present at 0 ppm. Residual ¹H signal from chloroform was seen at 7.24 ppm. The data were collected with Varian's Dbppste_cc sequence (right) at 600 MHz and processed in Mnova with the Bayesian method.

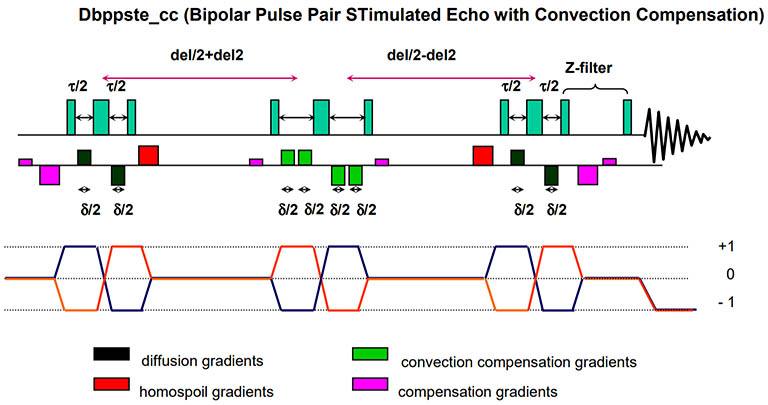Varian's Dbppste_cc pulse sequence with convection compensation. Convection is a macroscopic fluid flow resulting from a temperature gradient across the sample. It significantly distorts molecular diffusion and data quality. Convection compensation with gradient pulses minimizes this effect. However, the maneuver contains an extra stimulated echo step and therefore has an inherent, additional 50% signal attenuation with respect to its equivalent without convection compensation. It may not be suitable for samples with low SNR.

Tricks to minimize convection include disconnecting all air flow into the probe sample area, turning off temperature regulation and using a shorter sample with less volume.

Data Fitting to Extract Diffusion Constants

See this instruction for alternative steps in Mnova to extract the diffusion constants by fitting peak integrals.

References

Stejskal EO, Tanner JE. (1965) Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. J Chem Phys. 42, 288-92.
C.S. Johnson Jr (1999) Diffusion ordered nuclear magnetic resonance spectroscopy: principles and applications. Prog. Nucl. Magn. Reson. Spectrosc. 34, 203.
K.F. Morris, C.S. Johnson Jr. (1992) Diffusion-Ordered Two-Dimensional Nuclear Magnetic Resonance Spectroscopy. J. Am. Chem. Soc. 114, 3139.
G. Pages,a V. Gilard,b R. Martinob and M. Malet-Martino. (2017) Pulsed-field gradient nuclear magnetic resonance measurements (PFG NMR) for diffusion ordered spectroscopy (DOSY) mapping. Analyst, 2017, 142, 3771.
A. A. Marchione, E. F. McCord (2009) Spectral separation of gaseous fluorocarbon mixtures and measurement of diffusion constants by 19F gas phase DOSY NMR. J. Mag. Reson. 201, 34.
Varian user Guide: High-Resolution Diffusion-Ordered Spectroscopy (DOSY)

Updated, Jan-Feb 2019, Hongjun Zhou