NMR Theory and Techniques
Note: During training and assisting students and researchers, I often find it helpful to go over some
NMR theory which is usually picked up in bits and pieces sporadically over the years for most users. Evidently, this work has evolved
into a much bigger project in a short time. I hope these materials will spur more interest in NMR and
help all users, especially new ones, to broaden their skills and understanding of the NMR techniques. Some
data shown here are synthesized, perfect data for illustration purposes. The data are generated with in-house
written Tcl/Tk scripts, converted to nmrPipe binary
data, and then processed with Mnova. Many common NMR terminologies are
highlighted in bold. Since other aspects of the NMR techniques are covered in various lab classes, focus is given here
to better understanding the mathematical and physical basis of various NMR observations and techniques.
Some are very relevant to routine practice, especially in the design of NMR experiments and data interpretation.
-- Hongjun Zhou, @UCSB, 01/2019
"I insist upon the view that 'all is waves'." -- Erwin Schrödinger in Letter to John Lighton Synge (1959)
NOESY: Cross-Correlation Through Space
Nuclear Overhauser effect (NOE) is a magnetization exchange process between dipolar coupled spins. The energy term for
dipolar coupling between two close
magnetic dipoles (spins here) carries the distance dependence of 1/r3
where r is the distance between the two dipoles and ř is the unit vector. Note there are three separate angles
involved here in general: vector S1, vector S2, and vector r, in the
same reference frame. Molecular tumbling in solution causes the Hamiltonian to fluctuate.
In solution state, under isotropic (uniform) molecular rotation, the first-order time average of the Hamiltonian is zero
with no effect on the resonance frequency.
NOE is therefore
a second order effect of the energy term, contributing to spin relaxation and having a
distance dependence of 1/r6. The steep drop of the NOE intensity by 1/r6 means that
the effect is often only observable when the inter-spin distance is within ~ 5 Å.
From 2 Å to 5 Å, the
drop in NOE intensity is 244 times; from 3 Å to 5 Å, it's a drop of 21 times! With a good signal-to-noise
ratio (SNR) of 100 for a strong NOE peak for a distance of 3 Å, the weakest NOE would have a
SNR ~ 5, just above the level of detection and confidence. At 6 Å, the NOE carries a SNR of 1.5, essentially in the noise.
Therefore, good SNR is critical for detecting all possible NOEs and distances due to the wide range to cover. This is
equivalent to simultaneously detecting NMR signals from several molecules ranging from 200 mM to 1-10 mM in
the same sample. It is important that unless overall good SNR is attained, it is not sufficient
to draw solid conclusions based on observed or absent NOEs.
NOE intensity is also proportional to gyromagnetic ratios squared of the involved spin pair. This dependence
leads to NOE intensity of 256 times (γ4) and 10,000 times weaker between two 13C's
and two 15N's, respectively, than two 1H's, making the former ones unobservable by NMR. But, NOEs between 1H and
13C or 15N has much higher sensitivity, at 16 times and 100 times lower level than
1H-1H NOEs and can be useful. 1H-13C NOEs are used to enhance 13C
signal intensity in direct detection for example.
The mechanism of NOE is cross-relaxation between the spins, that is when one spin exchanges spin
states and relaxes towards the equilibrium state through the other spin. The dipolar interaction is a small perturbation (a few kHz)
to their Zeeman energy (several hundred MHz) states and the quantum perturbation theory applies. All transitions and rates
have been well studied and reported. Here we will explore a simpler physical picture of NOE. We start with characterizing
NOE through longitudinal relaxation (also called spin-lattice relaxation) along the static field direction.
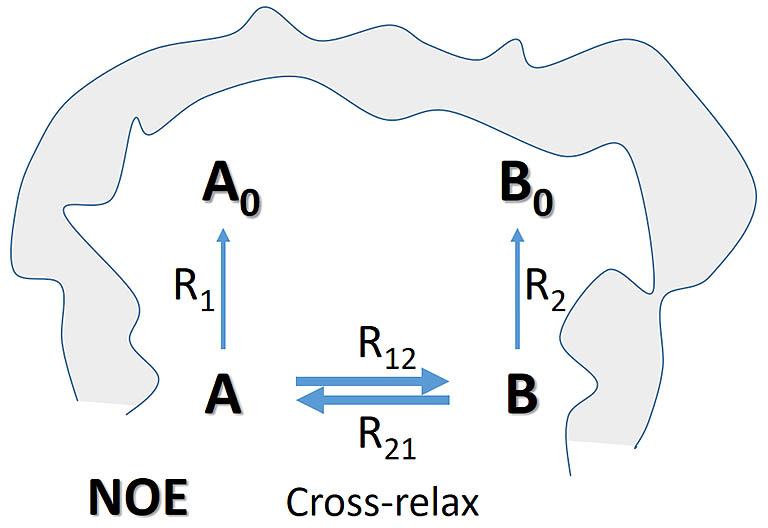
The figure above denotes all other relaxation pathways of the two spins with collective rates R1 and R2,
and their cross relaxation with rates R12 and R21. R1 and R2 are predominantly
auto (self)-relaxation through the dipolar coupling but also have other contributions not from the two involved spins.
The shaded area depicts the bulk lattice environment
that each spin may relax through in addition to the dominant, direct dipolar coupling. Auto-relaxation and
additional relaxation mechanisms which may involve other surrounding spins contribute leakage pathways and
are detrimental to NOE between two dipolar-coupled spins, weakening their NOE intensity. Note the similarity of the NOE mechanism to
the chemical exchange process discussed above. In fact, EXSY and NOESY are essentially the same
experiment both designed to study "exchange" between the spins, chemical exchange or otherwise. But, there is a critical
difference between chemical exchange and relaxation. Chemical exchange itself conserves the molecular and spin population,
but relaxation always takes the spins towards the equilibrium, lowers its magnetization state, and causes a loss to the
the spin magnetization of origin. This is reflected in the negative sign of the cross-relaxation term in the Solomon equations
that describe the relaxation processes.
Mimicking the Bloch-McConnell equations, the following Solomon equations apply under
auto-relaxation and cross-relaxations for Z magnetizations of spins A and B:
dMz1/dt = - R1*(Mz1 - A0) - R12*(Mz2 - B0) (1)
dMz2/dt = - R2*(Mz2 - B0) - R21*(Mz1 - A0) (2)
where A0 and B0 are the equilibrium magnetizations of A and B spins.
The chemical shift procession terms are absent because we have only the Z-axis magnetizations as it is the case during the
NOESY mixing or saturation period. Note the sign of the second term is negative, reflecting a loss of Mz
through the other spin.
Consider steady-state NOESY where one spin (spin A, M1) is selectively saturated with a weak
RF power and the effect on the other is observed. The saturation equalizes the up and down A spin population,
putting Mz1 = 0.
At the end of the A spin saturation, it has cross-relaxed
and B spin reaches equilibrium through NOE with A spin, therefore dMz2/dt = 0. We have the following from equation (2):
0 = - R2*(Mz2 - B0) + R21*A0
Solving for Mz2, we have:
Mz2 = (R2*B0 + R21*A0)/R2
For two 1H spins, B0 = A0. The steady-state B magnetization is simply:
Mz2 = (R2 + R21)/R2*B0 = B0 + R21/R2*B0 (3)
In a typical steady-state NOE difference experiment such as CYCLENOE
(see more details here), a difference spectrum with and without
spin saturation is taken, resulting in only peaks
affected by NOE transfer. Doing so to equation (3) above leads to an NOE enhancement of:
ΔMz2 = Mz2 - B0 = (R21/R2)*B0
NOE or NOE factor (or %NOE) is: NOE = R21/R2
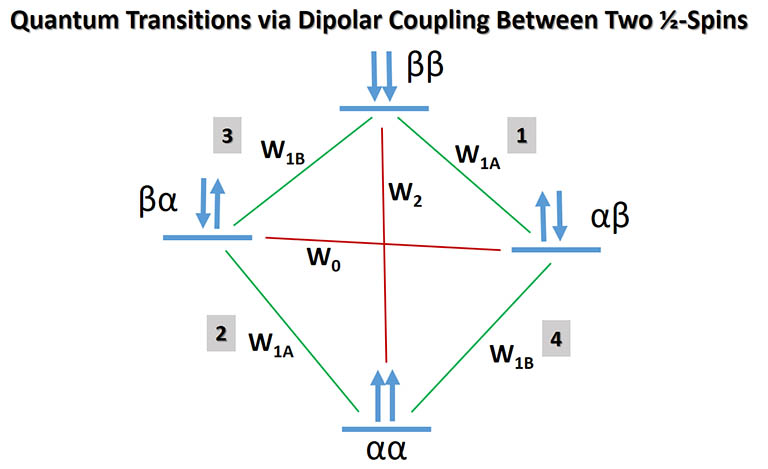
To relate the R rates with quantum state transition rates, we look at the following schematic diagram of the transitions involved.
We assume the γ's of both spins are positive leading to lower energies for the spin down states.
The two transitions highlighted in red with transition rates W2 and W0
are the cross relaxation pathways between spins A and B that
cause both spins to flip. That is, the flip of one spin is correlated with the flip of the other. If we sum up
the transition rates of all the pathways leading B spin to flip with or without A spin flip, these include transitions
3 and 4 (highlighted) and the cross-relaxations:
R2 = W0 + 2*W1B + W2
The total cross-relaxation rate R21 is:
R21 = W2 - W0
Note the negative sign for W0. This is due to the fact that when A spin in |βα> flips leading to
|αβ>, B spin goes opposite to the equilibrium direction which should be β to α in this case.
Now, we can express NOE with the quantum transition rates as:
NOE = (W2 - W0)/(W0 + 2*W1B + W2)
Taking the transition rate formulas and using "extreme narrowing" approximation for fast tumbling small molecules
where (ωτc)2 << 1 (ω is frequency of the transition, τc is the
rotational correlation time, timescale of molecular tumbling),
we have:
W1B ~ 3τc/r6, W0 ~ 2τc/r6, W2 ~ 12τc/r6
Plugging in these values, we obtain an NOE factor for two like (same type) spins in an NOE saturation experiment:
NOE = 50%
A few important aspects of the steady-state NOE need to be noted:
- The transition rates are functions of effective rotational correlation time. The results here only apply to
small molecules assuming fast Brownian motions.
- The steady-state NOE factor is independent of distance, therefore provides no precise spatial information. Such
more discrete distance information can only be obtained with transient NOE. Whenever possible,
transient NOESY, such as a typical 2D NOESY experiment, should be done in place of steady-state NOESY. See
discusion on this advantage below.
- This is the maximum NOE enhancement achievable because (1) we have assumed steady state equilibration is achieved
at B spin with saturation of A spin, and (2) we have ignored all other relaxation mechanisms such as with other protons and
nuclei or the bulk lattice. The leakage relaxation present in most cases almost always reduces NOE.
- The steady-state NOE between like-spins is always positive.
For unlike spins, such as 1H and 13C pair, an extra factor scaled with the population ratio of
the equilibrium states, γA/γB,
is needed in the NOE factor. We have:
Mz2 = (R2*B0 + R21*A0)/R2 =
B0 + (γA/γB)*(R21/R2)*B0
This leads to an NOE factor of NOE = (γA/γB)*(R21/R2)
= 0.5*γA/γB for a general dipolar coupled spin pair.
For {1H}13C, NOE = 2. This gain is commonly applied in 13C direct
detection by saturating 1H spins. For {1H}15N, the NOE is -5. The negative NOE for 15N
is from the negative γ of 15N spin. Saturating an adjacent 1H may weaken the 15N signal due
to other leakage relaxation pathways and is generally not applied.
Updated, Jan-Feb 2019, Hongjun Zhou
©2019 The Regents of the University of California. All Rights Reserved. UC Santa Barbara, Santa Barbara, CA 93106