NMR Theory and Techniques
Notes: During training and assisting students and researchers, I often find it helpful to go over some
NMR theory which is usually picked up in bits and pieces sporadically over the years for most users. Evidently, this work has evolved
into a much bigger project in a short time. I hope these materials will spur more interest in NMR and
help all users, especially new ones, to broaden their skills and understanding of the NMR techniques. Some
data shown here are synthesized, perfect data for illustration purposes. The data are generated with in-house
written Tcl/Tk scripts, converted to nmrPipe binary
data, and then processed with Mnova. Many common NMR terminologies are
highlighted in bold. Since other aspects of the NMR techniques are covered in various lab classes, focus is given here
to better understanding the mathematical and physical basis of various NMR observations and techniques.
Some are very relevant to routine practice, especially in the design of NMR experiments and data interpretation.
-- Hongjun Zhou, @UCSB, 01/2019
"I insist upon the view that 'all is waves'." -- Erwin Schrödinger in Letter to John Lighton Synge (1959)
Notes: Here we discuss some historical discoveries that led to the present understanding and applications of NMR techniques. We also
explore prospects of new exciting applications and the role of NMR played in other areas, including fundamental quantum physics.
I hope that this material helps spur interest for us to look into the past and future of NMR and some
areas not often covered in typical NMR classes or training. I'll continue to fill in parts of this section whenever
I have time to do so. -- H. Zhou, 2019
Overview
NMR theory and techniques have seen remarkable advances over the past few decades. The significance
of this progress is evidenced in part by a number of Nobel prizes awarded to the pioneers in NMR. These
include Isidor Rabi for the discovery of NMR in 1938 (awarded in 1944),
Felix Bloch and Edward Mills Purcell
for applying NMR techniques to study solution and solids (awarded in 1952), Richard R. Ernst for
developing pulsed FT NMR (awarded in 1991), Kurt Wüthrich for his pioneering work in
NMR of biological macromolecules (awarded in 2002),
and Paul Lauterbur and Peter Mansfield for the development of Magnetic Resonance Imaging (MRI) (awarded in 2003).
Together these represent one of the largest number of awards given to a narrow specific field of physical sciences.
Following several decades of advances in magnet and probe design, and software and automation development, collecting a simple NMR
spectrum can now be done in as quickly as a few minutes which often leads to immediate confirmation of the structure of a
small molecule compound. Auto- locking, shimming and tuning, and in certain setup, auto- sample change and
auto data processing have made data collection and interpretation user friendly and
almost trivial; they also enable automated data collection of a large number of samples often used during high throughput screening.
The convenience and usefulness of NMR has made NMR spectrometers widely accessible at most colleges and universities as well as many
chemical and pharmaceutical companies. NMR has become indispensable for many research and training programs. To the general public,
the noninvasive NMR techniques are even more widespread and impactful through the use of MRI
for disease diagnosis and functional studies.
If we name a few common applications of quantum physics in easily accessible technologies, NMR is near the top of the list.
For most users of an NMR spectrometer, the underlining quantum phenomena masked by classical macroscopic properties aren't obvious except
that most should know that spin is fundamentally a quantum property. However, there is no doubt that understanding
quantum physics is critically important in NMR theory and the design of complex pulse sequences that enable specific types of NMR data collection.
These pulse sequences carry the unmistaken names like Heteronuclear Single Quantum Correlation (HSQC), Heteronuclear Multiple
Quantum Correlation (HMQC), Double Quantum Correlation Spectroscopy (DQ-COSY), etc.
NMR is a fine example how such understanding, distinct from classical physics, has made possible
its widely successful application.
NMR is also an example where a semi-classical description remains very
intuitive and helpful. This hybrid treatment of NMR is justified by the fact that we measure macroscopic, ensemble properties of a large number of molecules
mostly under thermal equilibrium. Although each local, isolated spin system is a quantum system, on a larger scale, decoherence takes hold,
presenting a mostly classical system. One example is the macroscopic Bloch equations that describe the
relaxation of spins as two first-order processes, one in the transverse plane describing the loss of spin coherence, and the other along the
magnetic field direction returning the spins to thermal equilibrium. However, for the quantitative theoretical treatment and derivation of the spin relaxation
times at the microscopic level, when the relaxation mechanism invokes spin couplings,
multiple quantum correlations and transitions, a thorough quantum physics treatment becomes necessary.
Here we discuss several historical topics and the broader apllications of NMR theory and techniques.
Spin
NMR is a bridge to the microscopic quantum world of nuclear spins. Everything rotates or spins, and for those who don't, we give them spin (number) = 0.
The nucleus is composed of protons and neutrons, each carrying an internal spin (spin = 1/2). Protons and neutrons are further
composed of quarks in a sea of gluons where quarks
carry fractional charges and spin = 1/2, and the charge neutral gluons carry spin = 1.
Gluons mediate strong force and are equivalent to photons that mediate elecromagnetic force, both called bosons.
The spin-1/2 particles (i.e. protons, neutrons, quarks, electrons, ... etc) are called fermions. The properties and roles
of bosons and fermions are drastically different, to a large part due to their different spins and its quantum consequence.
The net spin of a nucleus is the result of all internal spins of the fundamental particles and their orbital angular momenta.
In the context of this discussion of NMR, "spin"
is an intrinsic property of an object, like mass, charge (but not velocity, not orbital angular momentum), and
it possesses a unique property that is fully defined by its rotational transformation. Here we distinguish spin (S) from orbital angular momentum (L)
which we use to refer to the rotational momentum of an object (i.e. electron) around a center (i.e. a nucleus). A quantum spin is simply
an indivisible part of life: it is there, built into the particles, intrinsic, inseparable, and forever. There are
profound reasons why the spin property is necessary to exist in the physical world as we know it. There is no accident.
The Divinity of Spin
"The aim of science is to make difficult things understandable in a simpler way; the aim of poetry is to state simple
things in an incomprehensible way. The two are incompatible." -- -- Paul A.M. Dirac quoted in A Scientific Biography (1990) by Helge Kragh
"Pick a flower on Earth and you move the farthest star." -- Paul A.M. Dirac
Despite Dirac's thinking that poetry is the opposite of science that always gets simple things much more complicated,
his statement above is absolutely poetic. It cuts into the core of our understanding of the physical world: the world as we see it is founded
upon a few, as few as possible, unified principles based on empirical evidence such as symmetry and equivalency.
It is these mathematically expressed principles that call into existence the spin properties in fundamental particles and matters built with them.
On a broader scale, as we solidify our understanding of the basic principles of nature, we come to realize that many separate rules, parts or variables of nature
we have proudly deciphered and declared, are all derived from the same origin and set of more fundamental principles. As we shrink down this set with
more knowledge and better understanding, we are surprised by how things are in fact related although they appear irrelevant to each other.
The divinity of spins could be drawn from Paul Dirac's genius derivation of the Dirac equation for relativistic quantum mechanics in 1928.
In the process of formulating a relativistically applicable, Lorentzian invariant, and realistic quantum wave equation,
Dirac intuitively overcame the difficulty of the Klein-Gordon equation for such an attempt and
replaced the nonrelativistic Schrödinger wave equation with its relativistic equivalent
operators in an unusual, Lorentzian invariant form.
This formulation under the required symmetry and energy conservation principles resulted in the introduction of Dirac spinors,
a 4-component wave function.
The embedded operators in the Dirac equation are 4X4 matrices in a 4-vector space that "coincidentally" share
similar properties with the Pauli (2X2) matrices already being used to describe newly discovered
spin-1/2 properties in the 2-vector space. Furthermore,
the orbital angular momentum (L) operator alone doesn't commute with the Hamiltonian in the Dirac equation, therefore is not conserved as a result.
However, "coincidentally", J = L + S, the sum of the orbital angular momentum and a straight 4X4 matrix operator (S) constructed from the Pauli spin matrices commutes with
the Hamiltonian, therefore is conserved and is ascribed to the total angular momentum operator. This extra operator that was needed to satisfy conservation
of the angular momentum was identified as the spin operator, an intrinsic operator of the particle. Therefore, strikingly,
spin is a natural consequence of the Dirac equation and in turn the consequence of the requirements from both quantum physics and relativity.
The necessary existence of spin property as required by the Dirac equation and its link to Einstein's special relativity is mysterious and
thought provoking: it is not obvious why spin needs to exist for resting or low-speed particles which do not
need to be described by relativistic physics at all. But, there is no accident. There is clearly no
sharp division between relativistic speed and "normal" speed; the speed of a reference frame is arbitrary, from infinitesimal up to the speed
of light. This calls for a coherent description with relativistic physics. There is no principal difference between resting, moving with an infinitesimal speed
or the speed of light in this regard. It is the symmetry principles of space and time that call for the existence of spin property. Dirac elevated
such basic principles to the forefront of theoretical physics:
"The important things in the world appear as the invariants (or more generally the nearly invariants, or quantities with simple transformation
properties) of these transformations. The things we are immediately aware of are the relations of these nearly invariants to a certain frame of reference,
usually one chosen so as to introduce special simplifying features which are unimportant from the point of view of general theory."
-- The Principles of Quantum Mechanics, 1930, P.A.M. Dirac
The 4-vector Dirac spinor for a spin-1/2 particle introduced two extra wave functions, more than what was
needed to describe the up and down states of one particle. These extra wavefunctions are symmetric with the other two but are
associated with negative energy terms. Dirac predicted that these were the antiparticle states. The first
antiparticle (positron) with the same mass and other properties but opposite charge with the particle (electron), was soon experimentally discovered
by Carl Anderson in 1932 in the electron (e-) and positron (e+) production during cosmic ray collisions. Undoubtedly, Dirac's work on relativistic quantum mechanics, based on simple principles and profound empirical
intuitiveness, was one of the brightest achievements
in theoretical physics.
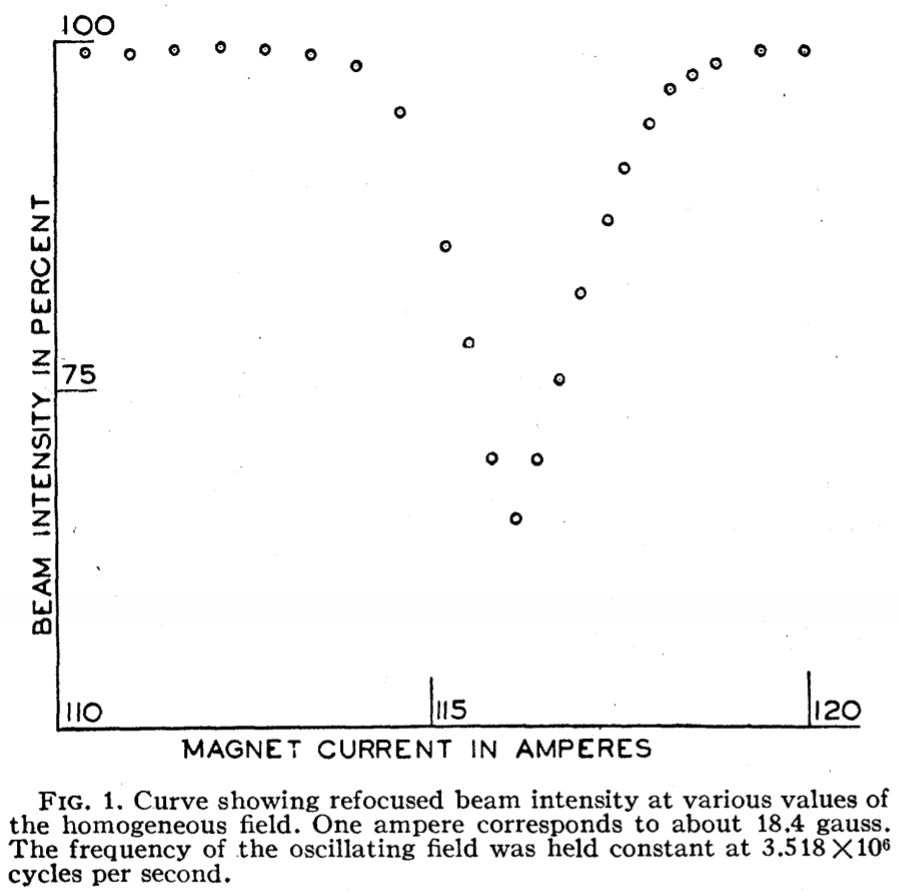
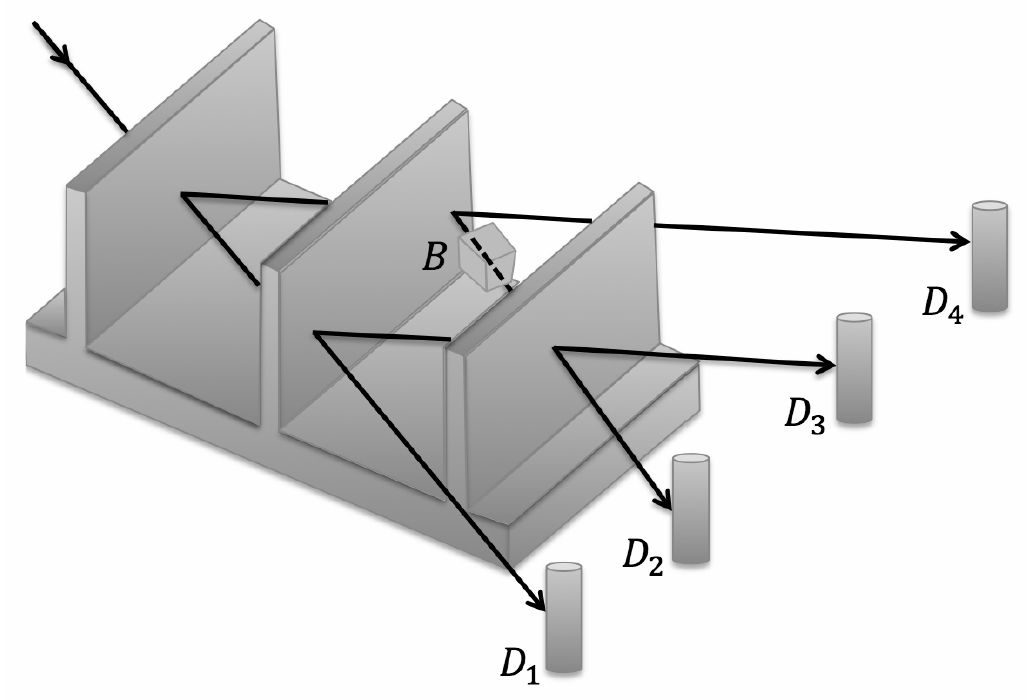
First published observation of NMR in 1938. In this
experiment, a beam of LiCl molecules were passed through two inhomogenous (non-uniform) magnetic fields.
The first field deflected the molecules according to their quantized magnetic moments. The
second field was oriented in the opposite direction of the first field to refocus the beam into a detector.
An additional uniform field was inserted in-between the two fields. The uniform field has no net forces
on the magnetic moments associated with the nuclear spins (the LiCl molecules were at ground state with no net electron spins)
and does not modify the beam flying path by itself.
However, when an oscillating magnetic field was applied
perpendicularly to this uniform field in the same area, the LiCl beam might be re-oriented, pulled, rendering
the subsequent refocusing field unable to refocus the beam for detection.
With the frequency of the oscillating field kept steady at either the Li + or Cl - nuclear spin frequency,
the static field was sweeped by changing the current (horizontal axis) of the coil. The minimum LiCl detection
occurred at the Larmor frequency (procession frequency of the nuclear spin around the static field)
that matches the frequency of the oscillating field when the induced re-orientation is at maximum.
The B field was ~ 0.02 Tesla (2000 Gauss), compared to a modern 500 MHz spectrometer at ~ 11.76 Tesla pruduced by a superconducting coil.
Rabi II, Zacharias JR, Millman S, Kusch P. A new method of measuring nuclear magnetic moment.
Physical Review. 53: 318. DOI: 10.1103/PhysRev.53.318
|
Quantum Nature of Spins
There is a clear distinction between spin and orbital angular momentum. An analogy is the difference
between the self-rotation (spin) of the Earth and its orbital rotation (orbital angular momentum) around the Sun. The former clearly
has no dependence on the presence of the Sun although the origin of Earth's self-rotation may. Additionally,
a quantum spin differs from a classical spin in more fundamental ways (i.e. see below about 4π periodicity of spin-1/2 particles). However, a quantum "spin" invokes the image of classical spin of an object: a spinning bicycle wheel, a
rotating magnet bar, or a pirouette by a ballet dancer. In the
classical picture, the life and state of a spin, including the interactions between spins and other objects, can be described precisely in space and
time coordinates and its trajectory is CONTINOUS. We now know that microscopic particles and objects do not
follow these classical physics rules; they stay in their discrete eigenstates or evolve in-between them. Only when we
subject them to observation in our physical world, we obtain a classical picture we are familiar with.
Historically, the discovery of the spin property landed strong support to space quantization in quantum physics. The spin
degree of freedom has no classical correspondence. It is discrete. For a particle with a spin number of 1/2 (spin = 1/2),
its spin value is either +1/2 or -1/2 when measured. For a particle with spin = 1, the measured value is +1, 0, or -1. These
discrete values share similarity with electric charges, but it is not a scalar. Rather, it is space and rotation related
and shares close similarity with a vector with rotational symmetry. However, it is a "quantum" vector,
not a classical one which affords spins and quantum angular momenta as a whole unique transformation properties.
The journal Nature
has compiled a list of the milestones for the discovery of spins.
Significantly, the historical Stern-Gerlach experiment (1922)
showed a beam of 109Ag (silver) atoms running through
an inhomogenous (non-uniform) magnetic field was split into two groups. This was inconsistent with both the one continously spread group prediction
from classical physics and the new quantum physics prediction with integer angular momentum assumed to L=0 (no split) or L=1
(three group split), leading Uhlenbeck and Goudsmit (1925, 1926)
to propose several years later that an electron carries a spin S=1/2 in order to give the two group split. Uhlenbeck and Goudsmit's
proposal provided a concrete physical basis to the "Pauli Exclusion Principle".
Wolfgang Pauli proposed in 1924-1925 "two-valuedness not describable classically" of an electron in his work on the
anomalous Zeeman splitting in the emission spectra of alkali metals in a
strong magnetic field. Pauli recounted the history of the "Pauli Exclusion Principle" in
his Nobel Prize lecture in 1946.
Now we know that in general, spin number can be a
half-integer with an increment of 1/2 whereas orbital angular momentum can only be an integer.
At the Dutch Physical Society in 1971, Goudsmit recounted
his experience as a physicist and the
history of electron spin discovery. van der Waals
prefaced the lecture notes he translated from Dutch with the following:
"... his could hardly be called a polished lecture; it was a grandiose artistic performance, full of wit and emotional
involvement. Goudsmit, then at the end of his scientific career, gave a very personal account of how chance and the guidance by
Ehrenfest, their far-sighted
supervisor, led him and Uhlenbeck to formulate their remarkable discovery."
Commonly Detected Nuclei
| Nucleus | Relative Frequency | Gyromagnetic Ratio
γ (106 rad⋅s-1⋅T-1) | Spin Number | Natural Abundance (%) |
| 1H | 1.0000 | 267.52219 | 1/2 | 99.9885 |
| 2H | 0.1535 | 41.065 | 1 | 0.0115 |
| 6Li | 0.1472 | 39.3717 | 1 | 7.59 |
| 7Li | 0.3886 | 103.977 | 3/2 | 92.41 |
| 11B | 0.3208 | 85.847 | 3/2 | 80.10 |
| 13C | 0.2515 | 67.2828 | 1/2 | 1.07 |
| 15N | - 0.1014 | - 27.116 | 1/2 | 0.368 |
| 19F | 0.9409 | 251.662 | 1/2 | 100.00 |
| 29Si | - 0.1987 | - 53.190 | 1/2 | 4.68 |
| 31P | 0.4048 | 108.291 | 1/2 | 100.00 |
*A detailed list can be found here. |
While many NMR phenomena can be fully or partly understood and described by classical physics, an area that requires a quantum physics interpretation of NMR is when dealing with coupled or transition states
where the non-continuous, quantized spin states have to be used. Consider an isolated spin pair 1H-13C situated in
a strong magnetic field. Both spins carry 1/2 spin numbers and are connected
by a single bond with an electron-mediated coupling interaction (called J or indirect coupling). The strong field separates the
spins into its eigenstates of up and down states from otherwise random orientations in the absence of the magnetic field.
Aside from a small energy difference in the up and down spin populations due to the small energy difference,
the two populations are nearly equal. The quantized nature of the spin states gives rise to split resonances from through-bond coupled spins.
Two resonances are observed in the 1H or 13C spectrum with a split of ~ 140 Hz.
The sharp split results from the two (up and down) quantum states of the through-bond coupled spin partner.
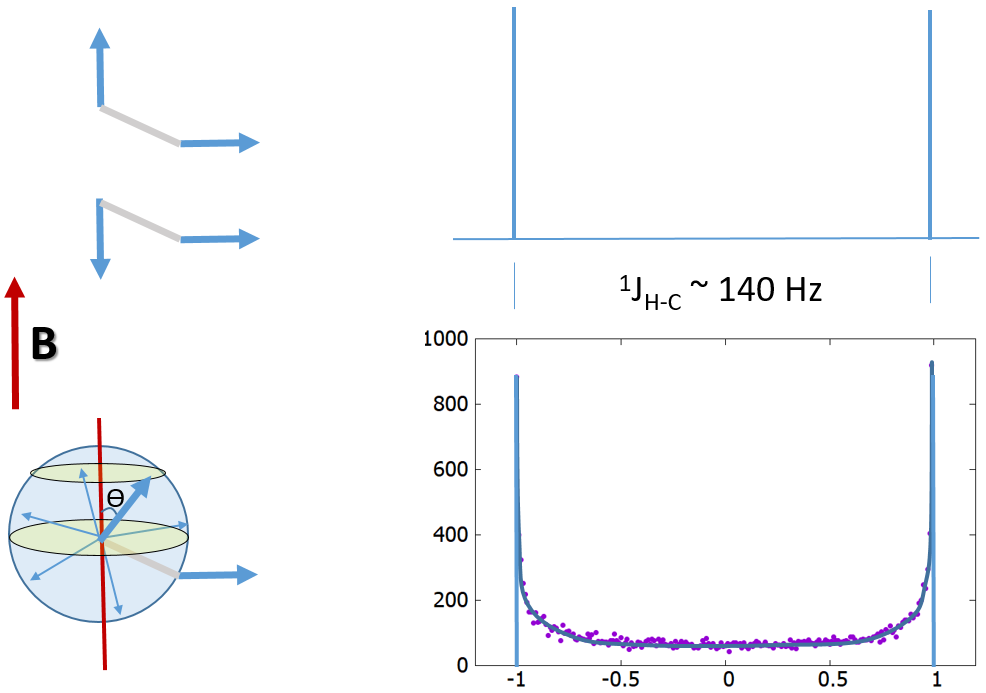
Quantized vs classical spin coupling. This
illustration shows the expected differences in the spectra from the split resonances due to
(1) top, quantized spin coupling to the up and down states of the coupling partner and (2) bottom,
classical continuous spread of polarization states of the coupling partner. Line broadening from
relaxation is omitted. Here we assume full isotropic, homogeneous molecular rotation in solution state.
The horizontal vector represents the spin being detected. It is
through-bond connected to the other spin. In the right figures, the vertical axis is intensity; the horizontal axis is relative frequency
centered around the isotropic chemical shift of the detected nucleus (1H or 13C).
In the classical picture, 20,000 random orientations of the spin vector from 0 to 180 degree
relative to the vertical B field are simulated. The coupling energy is ΔH ~ cos(θ)*sin(θ)
where sin(θ) accounts for the directional density weighting in the polar coordinates.
|
For the same coupled spin pair, a classical description of the magnetic moments associated with the spins is that their values
vary continuously from the maximum parallel to maximum anti-parallel alignment with the external magnetic field.
This continuity would lead to a much wider distribution of
the signal spread over the ~140 Hz range. The lineshape (or peak intensity profile) would resemble the powder spectrum
typically observed in solid-state NMR due to the spins' mostly random orientation in solution relative to the field.
This random orientation, only slightly biased by the small energy difference due to the interaction with the magnetic field,
mimics the random orientation of the spins in the solid-state powder. In another line of thinking,
the continuous orientation distribution, albeit with different probability density, can be approximated
with a system where many 1H couple to many 13C nuclei carrying the same chemical shifts
but a large number of varying J-coupling constants from 0 to 140 Hz between the coupling partners. Significant
broadening of the resonances and changes to the lineshape can be expected from the overlapping resonances.
In analytical NMR, the sensitivity of the nuclear spin resonance
frequency (chemical shift) to its chemical environment provides the foundation for NMR to be a powerful, sensitive
technique for structure elucidation. The interactions among spins and with the bulk environment provide
the fabric to uniquely associate spins with each other and with the environment through relaxation.
These interactions play a key role in through-bond, through-space, exchange correlated experiments, inter-molecular
interactions, and experiments measuring internal molecular dynamics. The quantitative, accurate mathematical description of nuclear spin
relaxation is an area where quantum mechanical understanding of the mechanism is needed. All
the quantum states, including all non-vanishing allowed transitions of various quantum orders, have to be accounted for.
These descriptions of the longitudinal relaxation time T1 and transverse relaxation time T2
are highly successful especially in the area of protein dynamics where relaxation parameters are measured and interpreted
on a residue by residue basis.
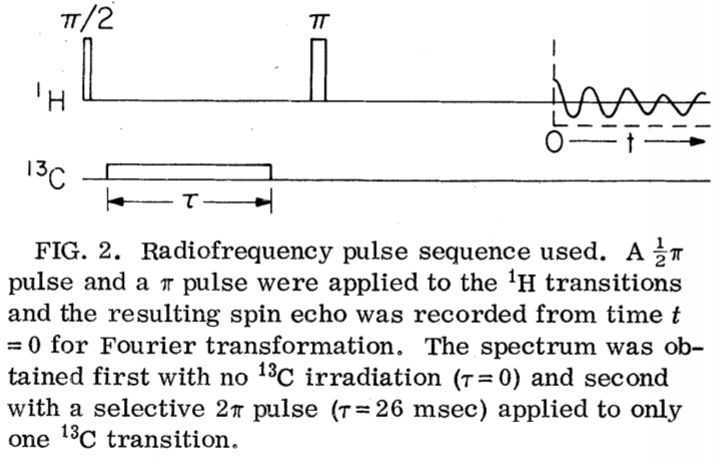
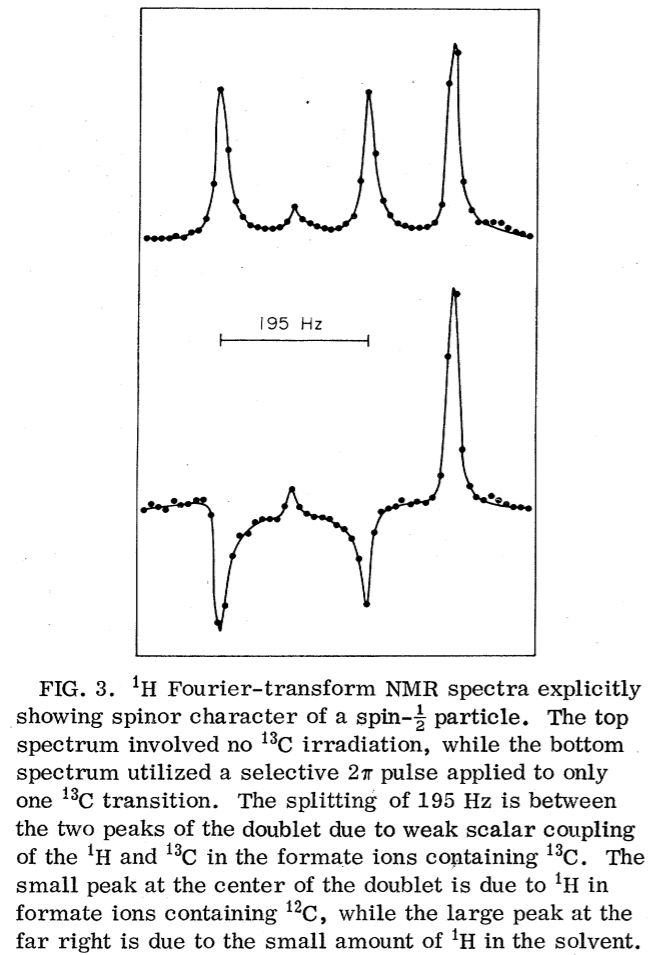
A Spinor Has 4π Rotational Periodicity
Spin-1/2 spins account for most nuclei detected by NMR. Spin-1/2 particles (called fermions), such as electrons, protons, and neutrons,
also form the bulk of our touchable universe and give condensed mass. They are mathematically classified as spinors.
One unique property of these spinor particles is that under rotation of 2π (360o), it doesn't
return to its original state: the sign of the wave function change by -1, that is ψ → - ψ. There is no classical physics equivalent of this odd behavior:
an object ends in upside down following a full turn of rotation. This sign change isn't detectable in most situations when measurements of quantum states
come down to population weighted distribution of the physical measurement. These probabilities ψψ†, equivalent to the squared
values of real numbers, are always positive. The avearge value of the measured quantum property A is <ψ|A|ψ> and it also
does not change with a sign inversion in ψ. To return to its original state, a 4π (720o) (or a mutltiple of 4π) rotation is needed for a
spin 1/2 particle. In comparsion, optical interference carries a periodicity of 2π,
reflecting the quantum wave behaviour of light with spin = 1.
However, when quantum interference is introduced before measurements, the phases of the wave packets are
physically meaningful properties that cause addition or subtraction between the wave functions. This quantum inteference
effect can be measured.
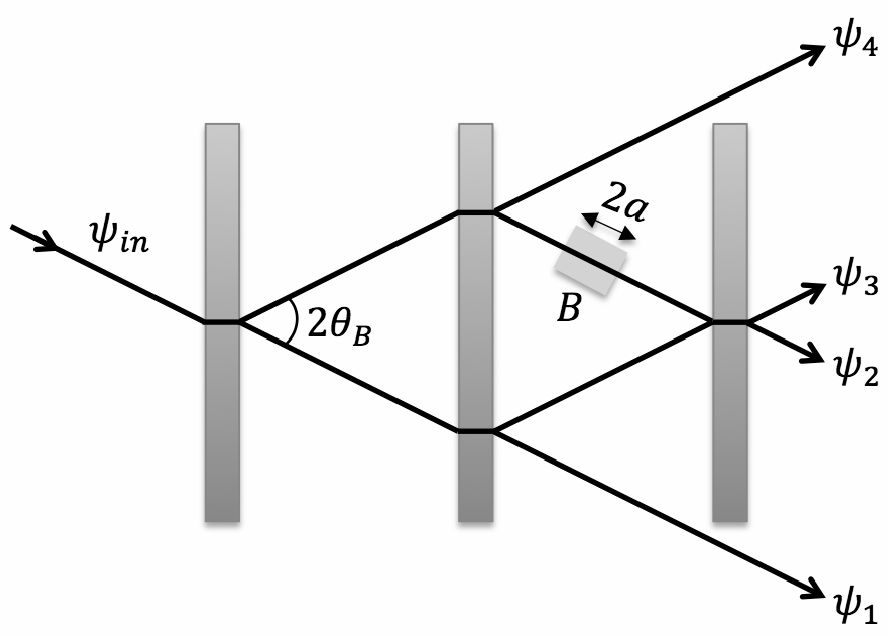
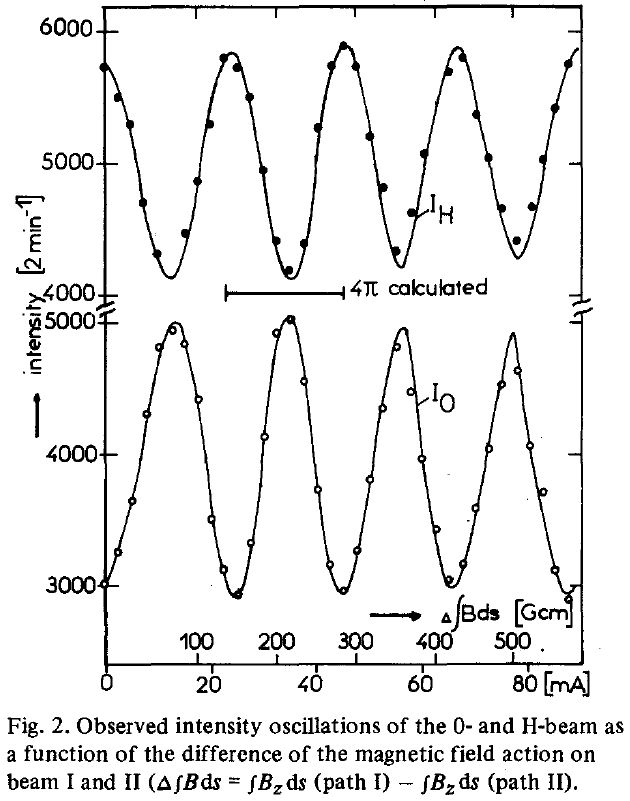
The 4π phase periodicty of a spinor has been first demonstrated using neutron interferometry, shedding light on fundamental quantum physics.
A neutron is a spin 1/2 particle. In 1975, two separate groups (H. Rauch et al, Phys. Lett. 54A, 425 (1975),
S. A. Werner et al, Phys. Rev. Lett. 35, 1053 (1975)) independently verified this physically meaningful phase change using a beam of neutrons
passing through a stack of silicon plates and observed the interference patterns of the neutrons. Subsequently, this was shown by other
techniques including NMR (M. E. Stoll, A. J. Vega, and R. W. Vaughan.
Phys. Rev. A 16, 1521 (1977)).
NMR Demonstration of Spinor Wave Sign Inversion Under 2π Rotation
NMR in Quantum Computing
Not surprisingly, NMR has played an important role in exploring the usefulness of the quantum wave
entanglement or interference through coherent interactions among spins. One
application is quantum computing,
a technique being explored to dramatically increase the present computing power and
revolutionize how we use computers in solving scientific problems presently unattainable.
Although more robust quantum computer systems have emerged,
the first experimental realization of a
quantum computer by scientists at IBM and Stanford University was
a
7 spin-1/2 (7 qubits) coupled nuclear spin system using solution state NMR. The quantum computer was
a custom-synthesized molecule, a perfluorobutadienyl iron complex, that contains five 19F and
two 13C spin-1/2 nuclei. The experiment (computation) was performed on a Varian Unity Inova 500 MHz NMR
spectrometer.
NMR, however, is not robust enough to offer large scale quantum computing power.
The very localized quantum coherence within a few chemical bonds and the decoherence effect from an ensemble of
molecules at thermal equilibrium pose an intrinsic limitation to a large set of qubits with NMR. Significant
advancement in quantum computing is being made with other techniques, including transmon qubits.
A recent breakthrough is highlighted by quantum supremacy achieved by
using a 53-qubit quantum circuit done by a team of scientists at UCSB and Google, Inc.
Magnetic Moments and Interactions with Magnetic Field
Each nucleus with a net non-zero spin number carries a magnetic moment:
μ = γI
where γ is the gyromagnetic ratio of the spin (see Table above). Note the ratio and the magnetic moment may be
positive or negative which leads to opposite sense of rotation of the spin in a magnetic field.
The interaction energy between the magnetic moment and an external magnetic field is:
E = - μ⋅B
For a positive magnetic moment, this energy leads to a small preferred parallel alignment (lower energy) with the field.
The force on a magnetic moment is the gradient of energy along a direction, the Z axis here:
F = - ∇E = - μ⋅∇Bz = - μz∂Bz/∂z
Therefore, if Bz is uniform along Z (or any other direction), there is no force
on the spin. However, in an inhomogeneous (non-uniform) magnetic field, the magnetic moment feels a force in proportion
to and along or opposite to the direction of the field gradient, depending on the sign of the magnetic moment.
Bending of a molecular beam in an inhomogeneous magnetic field was used extensively to study
the quantized magnetic moments of the molecules in the early years of the quantum physics (see Rabi's first NMR observation above as an example).
Modern solution NMR spectroscopy doesn't monitor the effects on the molecular trajectory induced by
forces on the magnetic moments.
However, there have been some recent, interesting applications with solid materials
using magnetic resonance force microscopy (MRFM).
Boltzmann Distribution and Magnetic Polarization
In an NMR experiment, we manipulate and measure the macroscopic magnetization. A typical sample is at the concentration of
a few hundred micromolar to many millimolar. For a detectable sample volume of ~ 0.3 mL (corresponding to the volume of
the 1.6 cm high RF active region in a 5 mm tube) and a concentration of 0.1 mM to 100 mM, this translates
into 3 x 10-8 mole to 3 x 10-5 mole, or 1.9 x 1016 to 1.9 x 1019 molecules (Avogadro's Constant = 6.022 x 1023/mole and also using
1 mM = 10-3 mole/L).
In a thermal bath around room temperature, the polarization of the nuclear spins follows
the Boltzmann distribution weighted by the partition function of the energy states. In the absence of
an external magnetic field, the spins have no preferred orientation, resulting in zero net magnetization.
In a strong static field, the energy difference between the up and down spin states leads to a small
preference for either the up or the down state depending on the sign of the magnetic moment.
According to the Boltzmann distribution, the occupation probability of the energy state (population) with Ei is:
ρi = e-Ei/kT/Σie-Ei/kT
where the summation in the denominator runs over all accessible energy states. Note that all "degenerate" eigenstates with the same energy
are counted separately and are implied in the summation. For example, for a two-spin system (each spin = 1/2) when total spin = 0, the two possible sub-states |+->, |-+>
are counted separated in both the denominator and the numerator.
We assume there are only two energy states here, corresponding to the up and down spin states of a single spin = 1/2. To estimate the degree of the spin alignment
with the field, lets first estimate the energy difference between the two states. We may resort to the energy equation above, or we can take a
short cut, knowing the resonance frequency is equivalent to this energy difference. For a 1H spin,
under the field corresponding to a 500 MHz resonance in the static field B = 11.76 Tesla, this energy is:
ΔE = ℏω = hν = 6.626 x 10-34 J⋅s x 500 x 106/s = 3.3 x 10-25 J
or, ΔE = ℏω = hν = 4.136 x 10-15 eV⋅s x 500 x 106/s = 2.1 x 10-6 eV
At T = 298 K (25 C), kT ~ 2.57 x 10-2 eV. Therefore, the ratio of the low to high energy state populations is:
ρ+/ρ- = eΔE/kT = e8.17 x 10-5 = 1.0000817
That is, the population difference of the two alignments or the net alignment is
(ρ+ - ρ-)/(ρ+ + ρ-) ~ 40 per million (0.004%).
In general, the polarization scales linearly with γ, field strength, and the spin number:
Δρ ∝ γ⋅I⋅B
Receiver and Free Induction Decay (FID)
The receiver coil, oriented in the XY plane perpendicular to the static field, receives the NMR signal.
From classical physics theory, we understand the rotating magnetic moments and associated fluctuating magnetic flux in the coil
induces an electric current, measured as a free induction decay (FID). Photons in the electromagnetic field are necessarily the sources
of the electromotive force (EMF) on the electrons in the coil producing the voltage. The source of these photos, however, has been debated.
This is somewhat surprising given that NMR techniques have been applied successfully and understood for the most part for decades.
One view is that EMF leading to NMR signals is attributed to physical photons emitted
(coherent spontaneous emission) as the spins rotate in the XY plane, a so called far-field effect, relative to direct induction,
a near-field first-order effect. The photon emission from accelerating, rotating magnetic moments is somewhat similar to the photon emission from
circulating electrons, called synchrotron radiation which is
widely used in high-resolution X-ray scattering.
Hoult et al. argued that
the far-field, direct photo emission contributes little (0.2%) to the measured EMF voltage while
the calculated near-field induction term matches well with the measurement (Hoult & Bhakar (1997) and Hoult and Ginsberg (2000)).
Direct photon emission was dismissed as the dominating mechanism of NMR signals and it was argued that virtual photons as formulated
in quantum electrodynamics (QED) are the source of EMF, and hence NMR signals in the receiver.
Books on NMR
There are many books that cover various aspects of NMR going back decades. Many up-to-date
coverge of specific topics can be found in reviews such as those published in
Progress in Nuclear Magnetic Resonance Spectroscopy. Here are a few authoritative books that have a
thorough and insightful treatment of broad subjects with sufficient theoretical materials
that dig deep into theoretical and some technical aspects of NMR. They may be difficult for beginners to read
but are highly recommended for anyone who seek a deeper understanding of NMR.
More general, easier to read NMR Books
Updated, Oct-Nov, 2019, Hongjun Zhou
©2019 The Regents of the University of California. All Rights Reserved. UC Santa Barbara, Santa Barbara, CA 93106